为了大家能更好理解Count the Cows的解法，我特地写了详细解题分析。
此问题使用到计算机科学非常重要思想：分治法（Divide-and-Conquer），就是分割问题、各个击破。将一个大问题，分割成许多小问题。如果小问题还是很难，就继续分割成更小的问题，直到问题变得容易解决。分割出来的小问题，称作子问题（subproblem）。解决一个问题，等价于解决所有子问题，解决子问题可以解决更大问题。
题目来源
USACO 2021 February Contest, Gold Problem 3. Count the Cows
思路
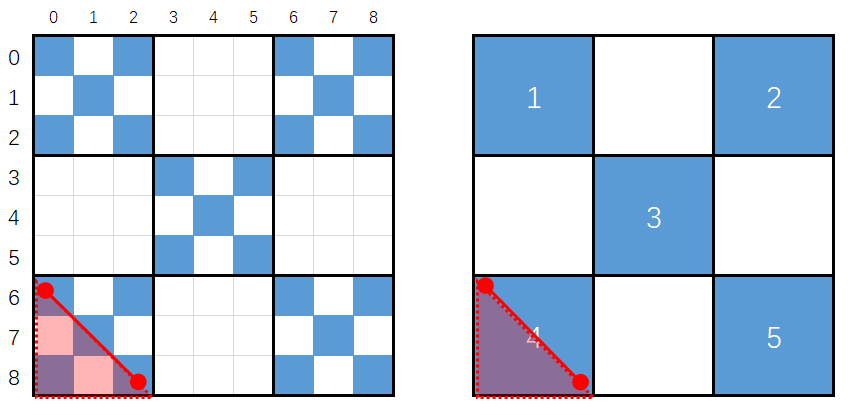
根据题目生成数据，发现在$3^i$长度的正方形内，称为$i$-维正方形A，奶牛位于正对角线和反对角线上的格子，如下红色和黄色部分。蓝色格子代表有奶牛，白色代表无奶牛。
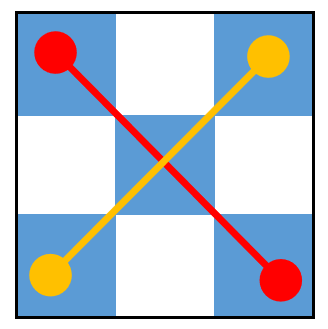
$i$-维正方形作为整体一个正方形，又拓展为$i+1$维正方形B。B的对角线和反对角线分别是A。每个$i$-维正方形的对角线上的小正方形是$i-1$-维正方形。这样可以无限拓展下去。例如：
1维正方形
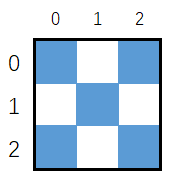$ {3\times3 \rightarrow 1\times1} \Rightarrow {3^1\times3^1 \rightarrow 3^0\times3^0}$
2维正方形
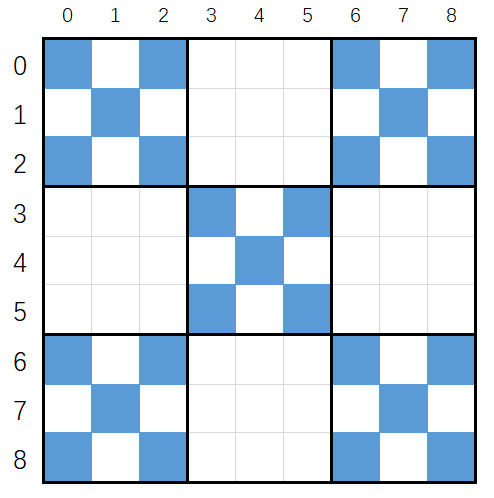$9\times9 \rightarrow 3\times3 \Rightarrow 3^2\times3^2 \rightarrow 3^1\times3^1$
3维正方形
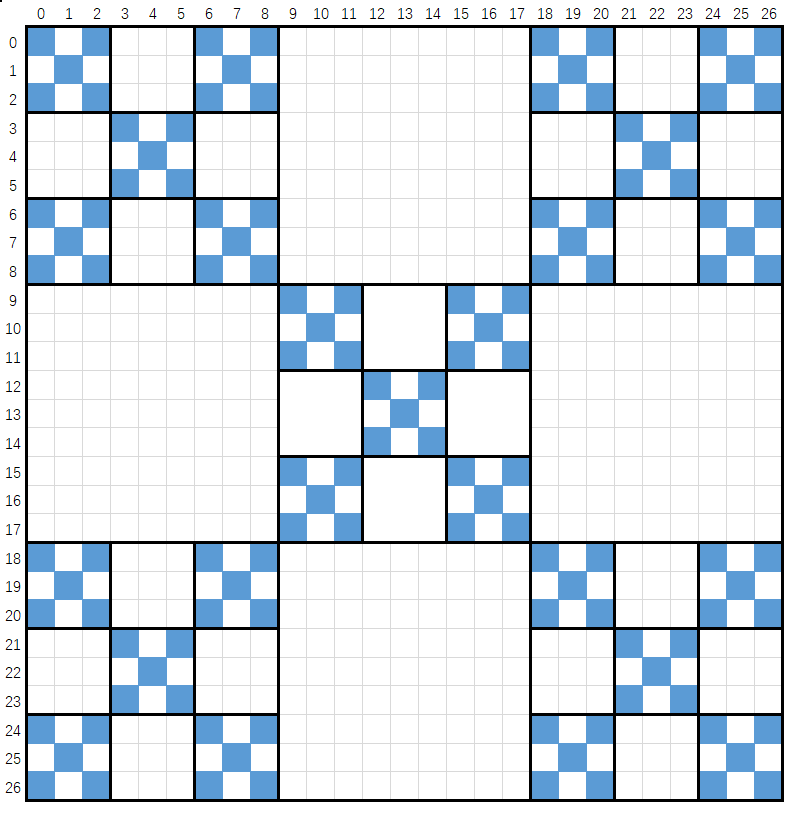$27\times27 \rightarrow 9\times9 \Rightarrow 3^3\times3^3 \rightarrow 3^2\times3^2$
$\Rightarrow 3^i \times 3^i \Rightarrow 3^{i-1} \times 3^{i-1}$
基础正方形 $3\times3 $
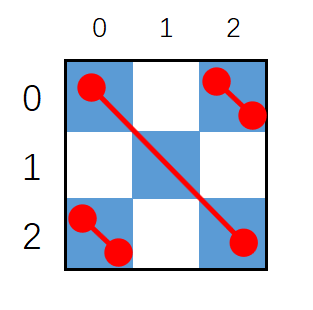
以下是以$(x,y)$为终点，在基础正方形$3\times3 $内，对角线经过蓝色格子的数量
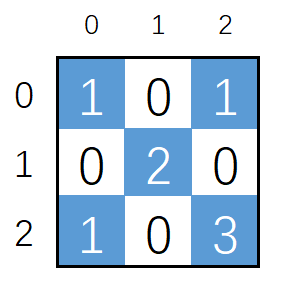
对称性
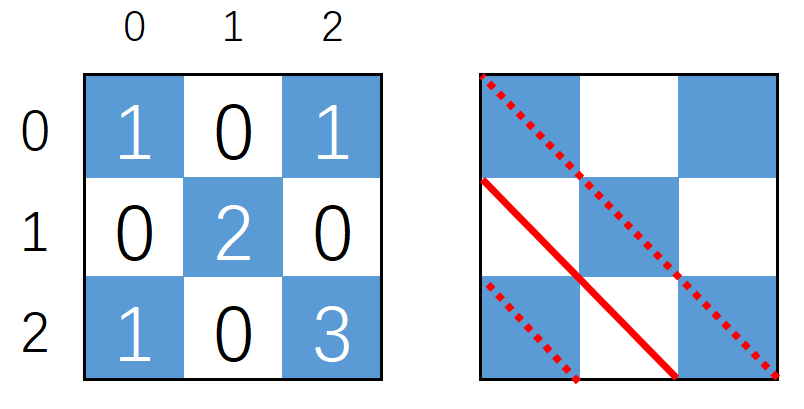
对角线$(x,y,d)$表示线段$(x,y) \rightarrow (x+d,y+d) $，进观察发现：对角线蓝色格子数：$(x,y,d)=(y,x,d)$,如下图：
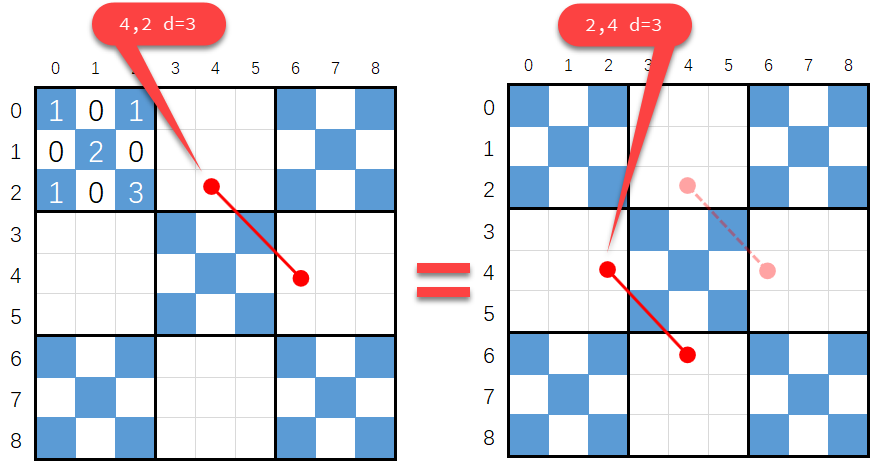
因此集中考虑黄色的区域，另外一半的区域可以转化成黄色区域的对角线
可叠加
如下图，对角线经过蓝色格子数量： 绿色$=$橙色$+$红色，因此
$ans_{x,y,d}=F_{x+d,y+d} - F_{x-1,y-1}$
$F_{x,y}$ 代表线段$A(0,y-x) \rightarrow B(x,y)$ 经过蓝色格子的数量
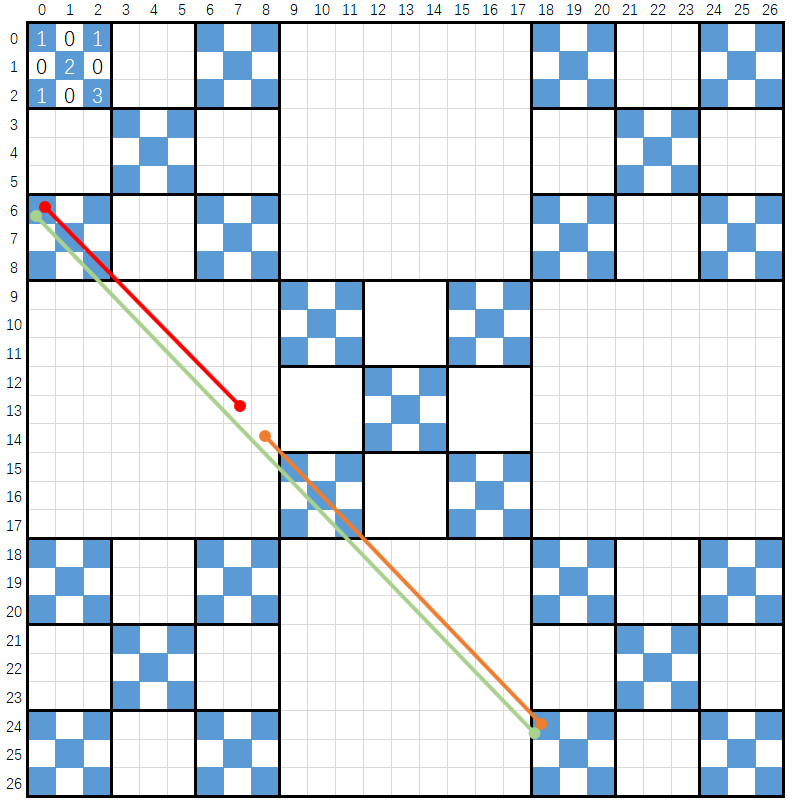
此时问题转换成：任意点(x,y)往对角线走，到左上边缘，经过蓝色格子的数量，如下图：
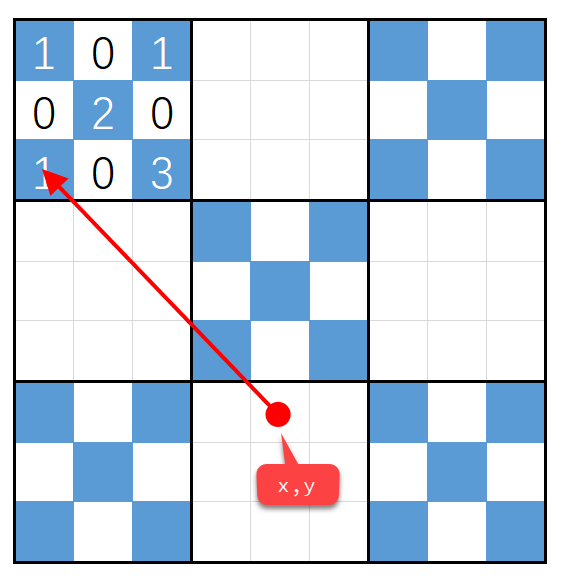
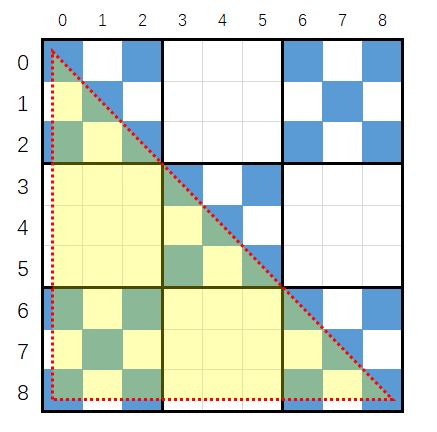
划分区域
$i$-维正方形在坐标$(0,3^{i-1})$处形成的对角线，不经过任何蓝色格子，$ans=0$。
在此处分割，分上、下两个区域，如下图红色区域和黄色区域。
- 黄色区域会经过$1$、$1+3$、$1+3+5$号蓝色格子
- 红色区域会经过$4$号蓝色格子
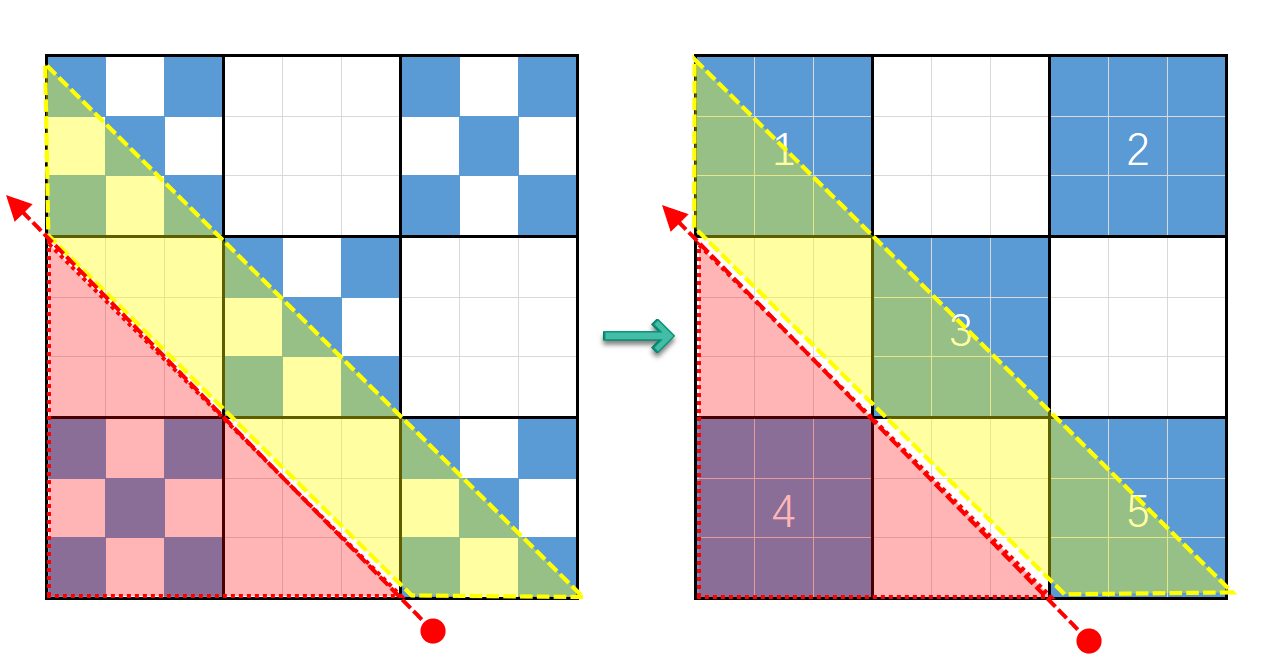
进一步细化，进观察以下图，点(x,y)在不同区域形成对角线：
- 在0区不经过任何蓝格子,$ans=0$
- 在1区会经过1号蓝格子
- 在3区会经过1+3号蓝格子
- 在5区会经过1+3+5号蓝格子
- 在4区会经过4号蓝格子
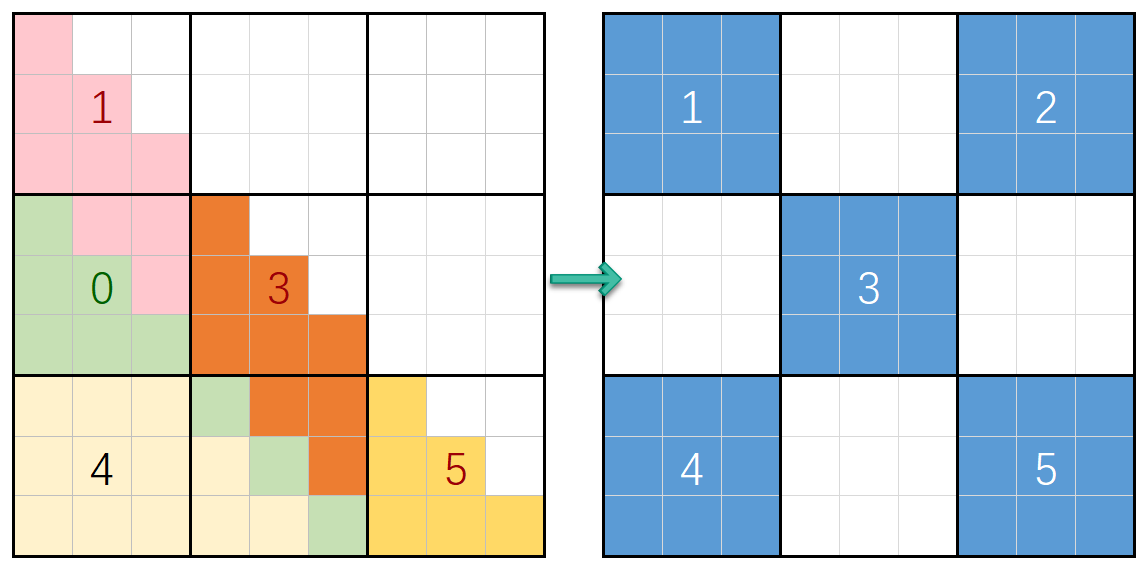
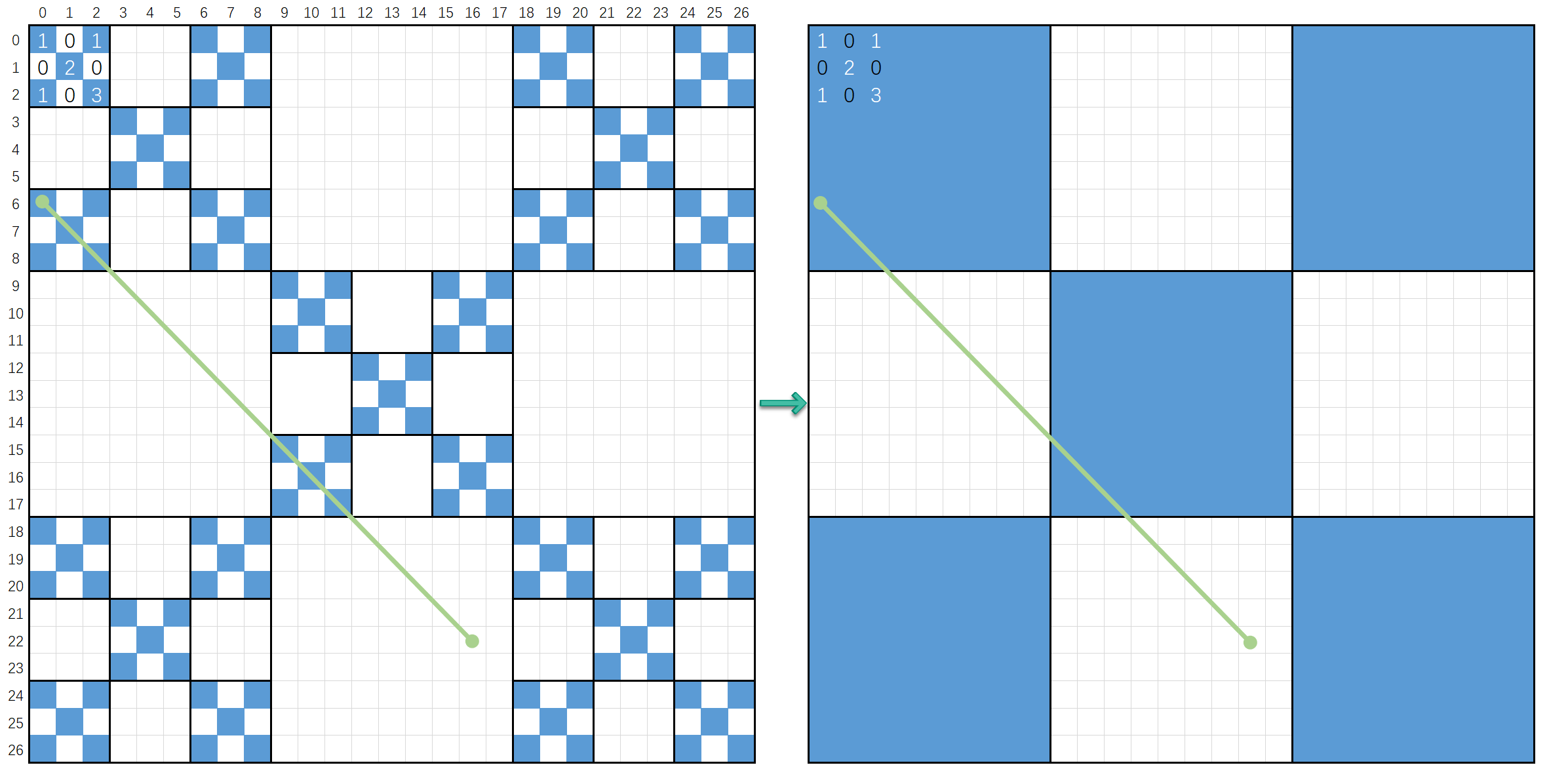
分治
-
对角线每经过一个正方形，都可拆分成最小单位的基础正方形$3\times3$，最终答案是由正方形 $3\times3$累加而得。
如下图：
-
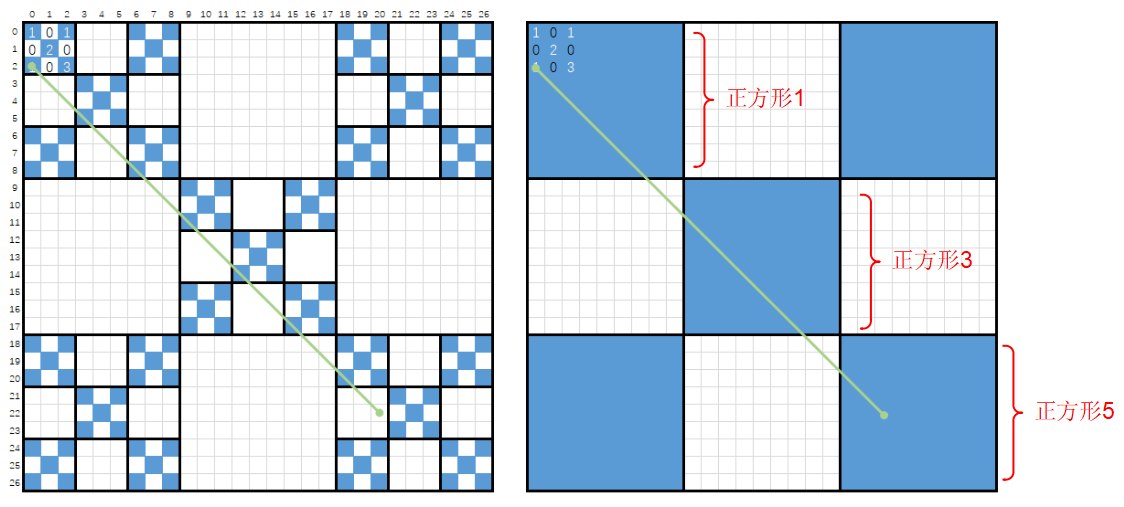
如下图,很明显
$ans=ans1+ans3+ans5$
正方形1,3都是完整的穿越的，因此
$ans=2*ans1+ans5$
算法拆分2部分，先计算穿越完整的正方形答案再计算不完整的正方形答案
算法设计
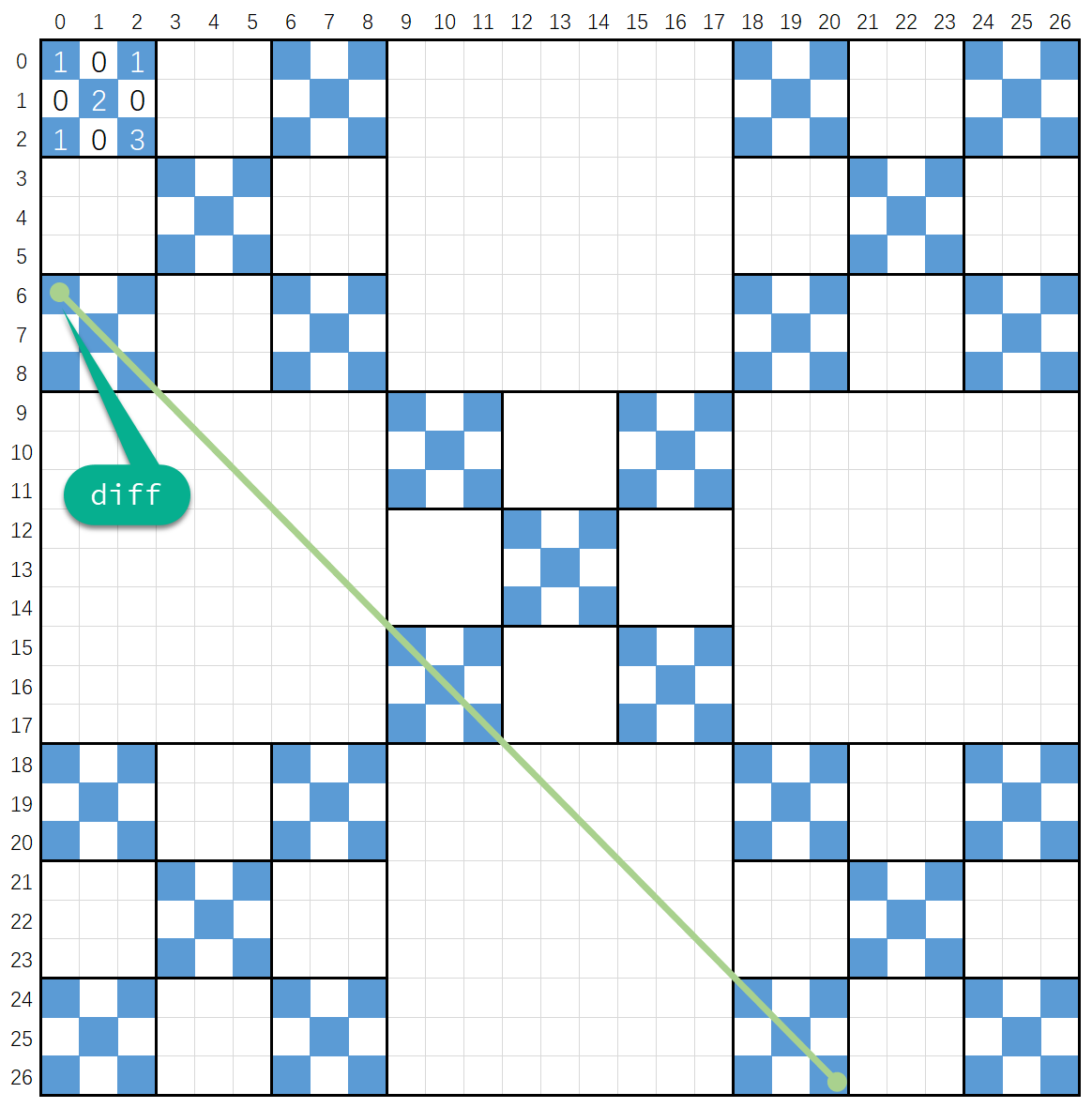
- 令 $diff=y-x$
- 对角线$(0,diff) \rightarrow (x,y)$在多大$3^i$的正方形？
1
2
3
4
5
6
7
8
9
10
|
//对角线(0,y-x)->(x,y)在多大3^i的正方形？
ill sqrLen(ill x, ill y)
{
ill max1 = max(x, y);
ill r = 1ll;
while (r <= max1)
r *= 3ll;
return r;
}
|
- 以点$(0,diff)$为对角线，也就是说直线 $y=x+diff$ 在长度是$n(n=3^i,n>diff)$的正方形内经过多少个蓝色格子？$n$必须能包住对角线。
1
|
ill fullSqrBlueCnt(ill diff, ill n)
|
- 情况一： 如果$n=1$或$n=3$
1
2
3
4
5
6
7
8
9
10
11
12
13
|
if(n==1ll)
{
return 1ll;
}
else if(n==3ll)
{
if(diff==0ll)
return 3ll;
else if(diff==1)
return 0ll;
else if(diff==2)
return 1ll;
}
|
- 情况二： $diff < \frac{n}{3}$,穿过$1,3,5 == 3 \times1$
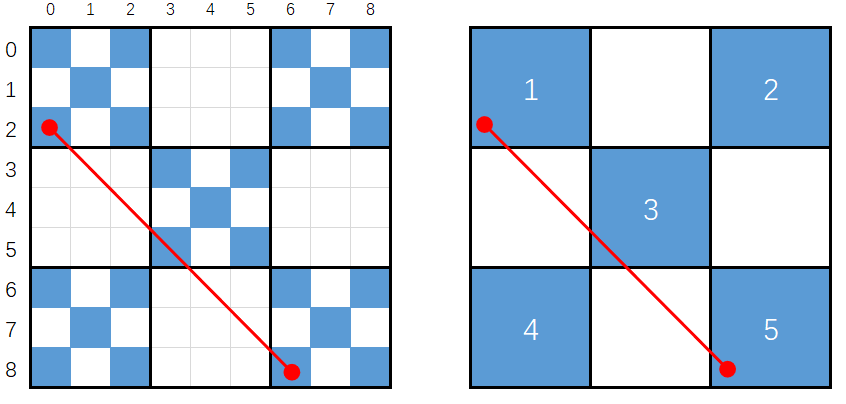
1
2
3
4
5
|
n /=3ll;
if (diff < n) //情况二：x<y<n,穿过1,3,5
{
return 3ll * fullSqrBlueCnt(diff, n);
}
|
- 情况三： $diff = \frac{n}{3}$,穿过空白格子
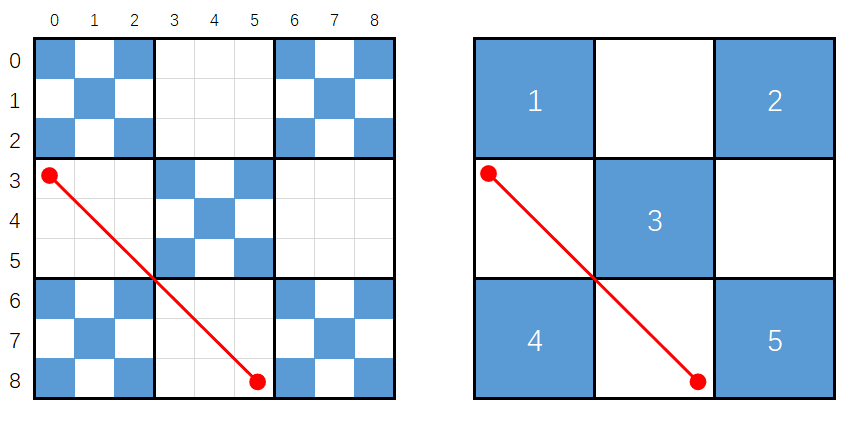
1
2
3
4
5
6
|
n /=3ll;
...
else if(diff==n) //情况三：穿过空白格子
{
return 0ll;
}
|
- 情况四： $\frac{n}{3} < diff < 2\times n$,穿过4号格子。处理办法：等同于在1号格子对角线的上部。计算走几步到达4号正方形，计算x,y坐标再递归调用情况二。
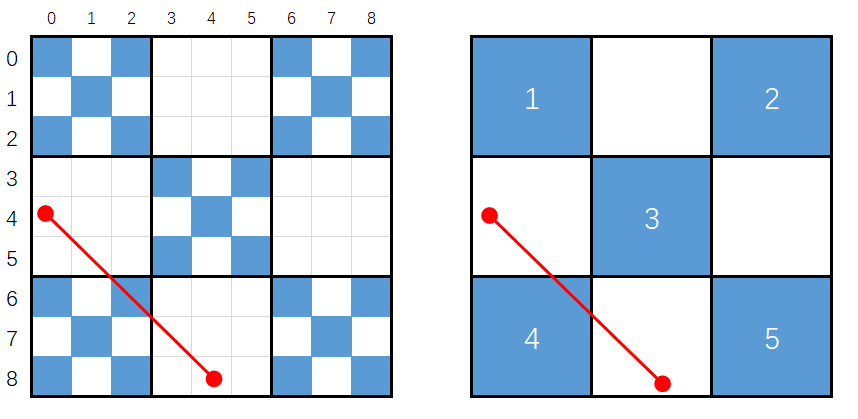
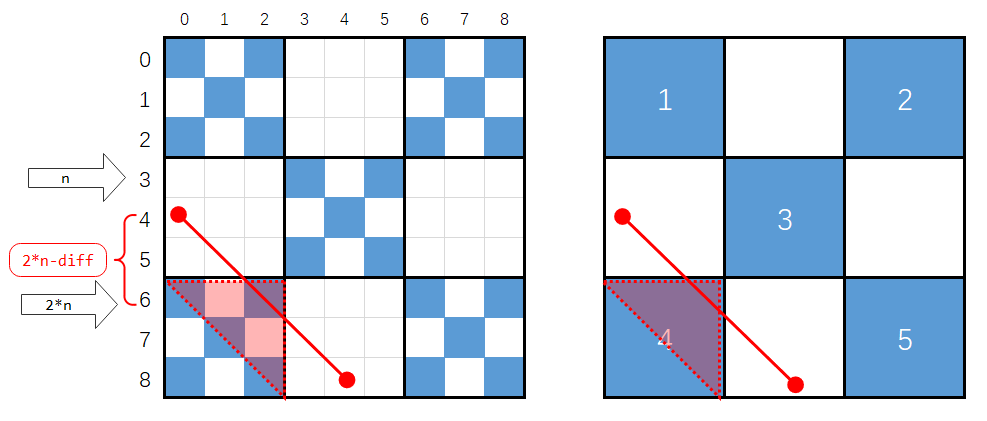
1
2
3
4
5
6
7
8
9
10
11
|
n /=3ll;
...
else if (diff < 2*n) //情况四：穿过4号格子，等同于在1号格子对角线的上部。计算走几步到达4号正方形，计算x,y坐标再递归调用情况二。
{
ill x1 = (2ll * n - diff);
ill y1 = 0ll;
if (x1 > y1)
swap(y1, x1);
return fullSqrBlueCnt(y1 - x1, n);
}
|
- 情况五：等同情况一，穿过4号格子，处理办法：等同于在1号格子对角线或者对角线的下部
1
2
3
4
5
6
7
|
n /=3ll;
...
else //情况五：等同情况一，穿过4号格子，处理办法：等同于在1号格子对角线或者对角线的下部
{
return fullSqrBlueCnt(diff % n, n);
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
//在长度是n的正方形内，(0,diff) 开始的对角线，在n长度的正方形经过了多少个蓝色格子
ill fullSqrBlueCnt(ill diff, ill n)
{
//情况一：
if(n==1ll)
{
return 1ll;
}
else if(n==3ll)
{
if(diff==0ll)
return 3ll;
else if(diff==1)
return 0ll;
else if(diff==2)
return 1ll;
}
n /=3ll;
if (diff < n) //情况二：x<y<n,穿过1,3,5
{
return 3ll * fullSqrBlueCnt(diff, n);
}
else if(diff==n) //情况三：穿过空白格子
{
return 0ll;
}
else if (diff < 2*n) //情况四：穿过4号格子
{
ill x1 = (2ll * n - diff);
ill y1 = 0ll;
if (x1 > y1)
swap(y1, x1);
return fullSqrBlueCnt(y1 - x1, n);
}
else //情况五：等同情况一，穿过4号格子，处理办法：等同于在1号格子对角线或者对角线的下部
{
return fullSqrBlueCnt(diff % n, n);
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
|
//在长度是n的正方形内，线段(0,y-x)->(x,y)经过了多少个蓝色格子
ill sum(ill x, ill y, ill n)
{
if (x > y)
swap(x, y);
if (n == 1)
return 1ll;
else if (n == 3ll)
return baseSqr[x][y];
ill topLeftSquareLen = n / 3ll; //左上角正方形大小3^(i-1)
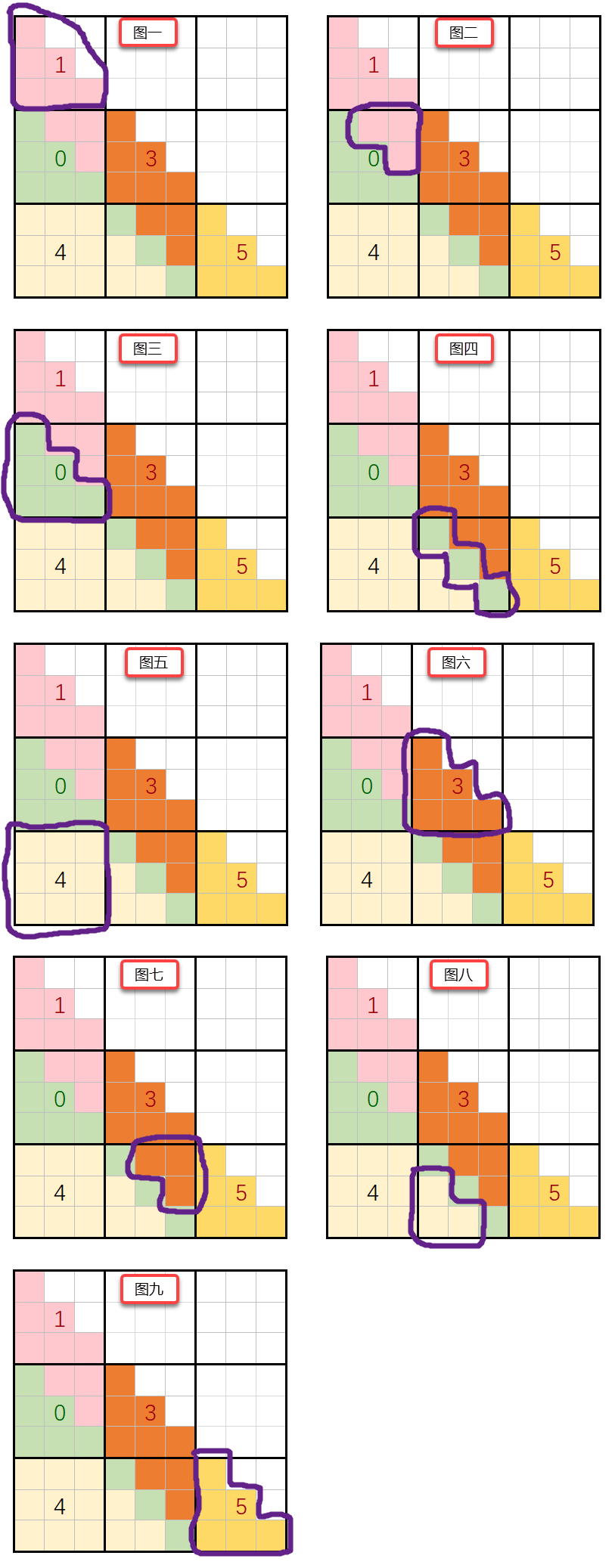
if (y < topLeftSquareLen) //图一
{
return sum(x, y, topLeftSquareLen);
}
else if (x < topLeftSquareLen)
{
if (y < x+ topLeftSquareLen) //图二
{
return fullSqrBlueCnt(y-x, topLeftSquareLen);
}
else if (y >= x + topLeftSquareLen && y < 2ll * topLeftSquareLen) //图三
{
return 0ll;
}
else //图五 ,y >= 2ll * topLeftSquareLen
{
return sum(x, y%topLeftSquareLen, topLeftSquareLen);
}
}
else if (y == x + topLeftSquareLen) //图四
{
return 0ll;
}
else if (x < 2ll*topLeftSquareLen)
{
if (y < 2ll * topLeftSquareLen) //图六
{
return fullSqrBlueCnt(y-x, topLeftSquareLen) + sum(x%topLeftSquareLen, y%topLeftSquareLen, topLeftSquareLen);
}
else if (y < x + topLeftSquareLen) //图七
{
return 2ll*fullSqrBlueCnt(y-x, topLeftSquareLen);
}
else //图八
{
ill y1=2ll*topLeftSquareLen;
ill x1=x-(y-y1);
y1 %=topLeftSquareLen;
x1 %=topLeftSquareLen;
if(x1>y1)
swap(x1,y1);
return fullSqrBlueCnt(y1-x1, topLeftSquareLen);
}
}
else //图九
{
return 2ll*fullSqrBlueCnt(y-x, topLeftSquareLen)+sum(x%topLeftSquareLen, y%topLeftSquareLen, topLeftSquareLen);
}
}
|
以下各种情况对应代码$if$判断情况
