概念
最长公共子序列(LCS)是一个在一个序列集合中(通常为两个序列)用来查找所有序列中最长子序列的问题。这与查找最长公共子串的问题不同的地方是:子序列不需要在原序列中占用连续的位置 。最长公共子序列问题是一个经典的计算机科学问题,也是数据比较程序,比如Diff工具,和生物信息学应用的基础。它也被广泛地应用在版本控制,比如Git用来调和文件之间的改变。
https://zh.wikipedia.org/wiki/最长公共子序列
https://en.wikipedia.org/wiki/Longest_common_subsequence_problem
案例
参考《算法导论》例子P222
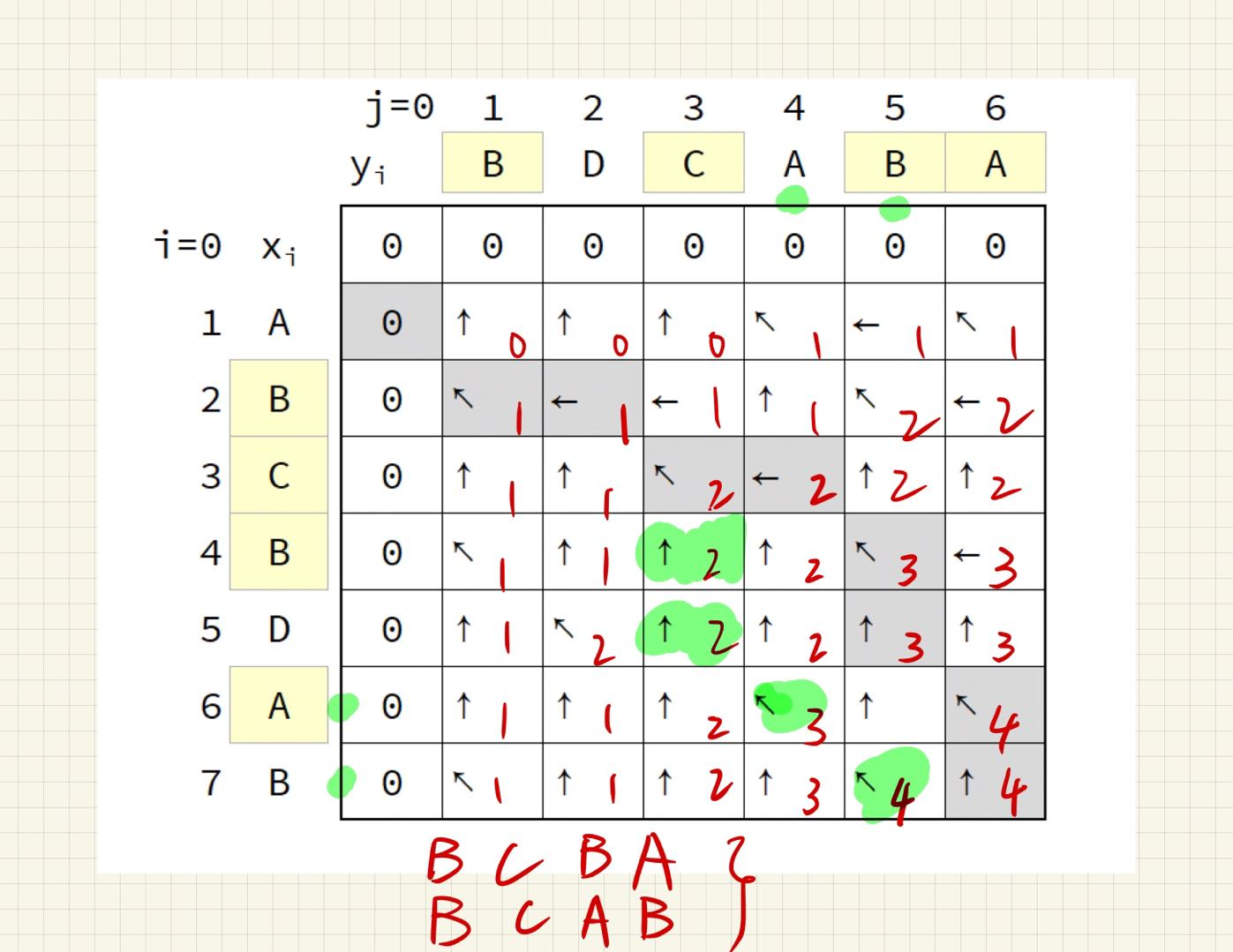
方法1:暴力递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
/**暴力计算LCS(递归版)
*
* @param {string} word1 : 【输入】第一个字符
* @param {string} word2 : 【输入】第二个字符
* @param {int} i : 【输入】第一个字符长度
* @param {int} j : 【输入】第二个字符长度
* @return {int} : 【返回】LCS长度
*/
int LCSRecursion(string & word1, string & word2, int i, int j)
{
if (i == 0 || j == 0)
{
return 0;
}
else if (word1[i - 1] == word2[j - 1])
{
return LCSRecursion(word1, word2, i - 1, j - 1) + 1;
}
else
{
return max(LCSRecursion(word1, word2, i - 1, j),
LCSRecursion(word1, word2, i, j - 1));
}
}
|
方法2:动态规划DP版本(正常数组),仅计算长度。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
/**LCS DP版本(正常数组),仅计算长度。
*
* @param {string} word1 : 【输入】第一个字符
* @param {string} word2 : 【输入】第二个字符
* @return {int} : 【返回】LCS长度
*/
int LCSLength(string & word1, string & word2)
{
int n = word1.length();
int m = word2.length();
vector<vector<int>> dp(n + 1, vector<int>(m + 1));
//初始化空字符串的情况
for (int i = 1; i <= n; ++i)
dp[i][0] = 0;
for (int j = 1; j <= m; ++j)
dp[0][j] = 0;
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j)
if (word1[i - 1] == word2[j - 1])
dp[i][j] = dp[i - 1][j - 1] + 1;
else
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
return dp[n][m];
}
|
方法3:动态规划DP版本(正常数组),计算长度和路径。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
|
/**LCS DP版本(正常数组),计算长度和路径
*
* @param {string} word1 : 【输入】第一个字符
* @param {string} word2 : 【输入】第二个字符
* @param {vector<vector<string>>} path : 【返回】路径数组
* @return {int} : 【返回】LCS长度
*/
int LCSDp(string & word1, string & word2, vector<vector<string>> & path)
{
int n = word1.length();
int m = word2.length();
//dp[i][j] 截止到word1前i项,word2前j项的最长的LCS长度(最优解)
vector<vector<int>> dp(n + 1, vector<int>(m + 1));
path.resize(n + 1, vector<string>(m + 1));
// 初始化空字符串的情况
for (int i = 1; i <= n; ++i)
{
dp[i][0] = 0;
}
for (int j = 1; j <= m; ++j)
{
dp[0][j] = 0;
}
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= m; ++j)
{
if (word1[i - 1] == word2[j - 1])
{
dp[i][j] = dp[i - 1][j - 1] + 1;
path[i][j] = "↖";
}
else
{
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
if (dp[i - 1][j] >= dp[i][j - 1])
{
path[i][j] = "↑";
}
else
{
path[i][j] = "←";
}
}
}
}
return dp[n][m];
}
|
方法4:打印输出路径(正常数组)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
/**打印输出路径(正常数组)
*
* @param {vector<vector<string>>} path : 【输入】路径数组
* @param {string} word1 : 【输入】第一个字符
* @param {int} i : 【输入】第一个字符长度
* @param {int} j : 【输入】第二个字符长度
*/
void printLCS(vector<vector<string>> & path, string & word1, int i, int j)
{
if (i == 0 || j == 0)
return;
if (path[i][j] == "↖")
{
printLCS(path, word1, i - 1, j - 1);
cout << word1[i - 1] << " ";
}
else if (path[i][j] == "↑")
{
printLCS(path, word1, i - 1, j);
}
else
{
printLCS(path, word1, i, j - 1);
}
}
|
方法5:DP版本(滚动数组),仅计算长度。空间复杂度优化,时间复杂度一样。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
/**LCS DP版本(滚动数组),仅计算长度。空间复杂度优化,时间复杂度一样
*
* @param {string} word1 : 【输入】第一个字符
* @param {string} word2 : 【输入】第二个字符
* @return {int} : 【返回】LCS长度
*/
int LCS2Length(string & word1, string & word2)
{
int n = word1.length();
int m = word2.length();
int m1 = max(n, m);
vector<vector<int>> dp(2, vector<int>(m1 + 1));
//初始化空字符串的情况
for (int j = 1; j <= m1; ++j)
{
dp[0][j] = 0;
dp[1][j] = 0;
}
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= m; ++j)
if (word1[i - 1] == word2[j - 1])
dp[i % 2][j] = dp[(i - 1) % 2][j - 1] + 1;
else
dp[i % 2][j] = max(dp[(i - 1) % 2][j], dp[i % 2][j - 1]);
return dp[n % 2][m];
}
|
方法6:DP版本(滚动数组),计算长度和路径。空间复杂度优化,时间复杂度一样。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
|
/**LCS DP版本(滚动数组),计算长度和路径。空间复杂度优化,时间复杂度一样
*
* @param {string} word1 : 【输入】第一个字符
* @param {string} word2 : 【输入】第二个字符
* @param {vector<vector<string>>} path : 【返回】路径数组
* @return {int} : 【返回】LCS长度
*/
int LCS2Dp(string & word1, string & word2, vector<vector<string>> & path)
{
int n = word1.length();
int m = word2.length();
int m1 = max(n, m);
vector<vector<int>> dp(2, vector<int>(m1 + 1));
path.resize(n + 1, vector<string>(m + 1));
// 初始化空字符串的情况
for (int j = 1; j <= m1; ++j)
{
dp[0][j] = 0;
dp[1][j] = 0;
}
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= m; ++j)
{
if (word1[i - 1] == word2[j - 1])
{
dp[i % 2][j] = dp[(i - 1) % 2][j - 1] + 1;
path[i][j] = "↖";
}
else
{
dp[i % 2][j] = max(dp[(i - 1) % 2][j], dp[i % 2][j - 1]);
if (dp[(i - 1) % 2][j] >= dp[i % 2][j - 1])
{
path[i][j] = "↑";
}
else
{
path[i][j] = "←";
}
}
}
}
return dp[n % 2][m];
}
|
UVA-1045 - Longest Common Subsequence
使用以上办法都可以
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
int main()
{
//UVA 10405 - Longest Common Subsequence
while (fin.good())
{
string x = "";
string y = "";
getline(fin, x);
getline(fin, y);
fout << LCS2Length(x, y) << "\n";
}
return 0;
}
|
测试LCS代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
|
int main()
{
//算法导论例子P222
string x = "ABCBDAB";
string y = "BDCABA";
vector<vector<string>> path;
cout << setw(14) << "X: " << x << '\n';
cout << setw(14) << "Y: " << y << '\n';
cout << setw(14) << "LCSRecursion: ";
cout << LCSRecursion(x, y, x.length(), y.length()) << '\n';
cout << setw(14) << "LCSDp: " << LCS2Dp(x, y, path) << '\n';
cout << setw(14) << "LCS: ";
//构造LCS
printLCS(path, x, x.length(), y.length());
//输出过程
cout << "\n输出过程\n";
cout << "--------------------\n";
cout << " ";
for (auto k : y)
cout << k << " ";
int k = 0;
for (auto i : path)
{
int l = 0;
if (k > 0)
cout << x[k - 1] << " ";
for (auto j : i)
{
if (l > 0)
cout << j << " ";
++l;
}
cout << '\n';
++k;
}
cout << "--------------------\n";
cout << "完成" << '\n';
return 0;
}
|
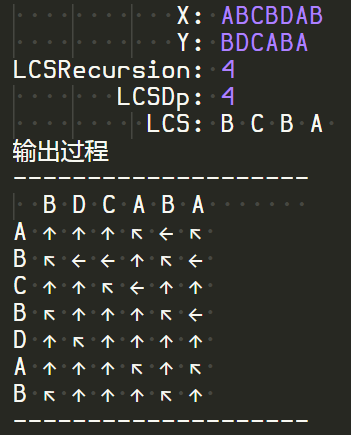
测试结果